What do your students do when faced with a math problem they don't know how to solve? Most students give up pretty quickly. At best, they seek help from another student or the teacher. At worst, they shut down, seeing their failure as more evidence that they just aren't good at math. Neither of these behaviors will serve students in the long run. Inevitably, someday, every one of your students will encounter problems that they will not have explicitly studied in school and their ability to find a solution will have important consequences for them.
In the Common Core State Standards for Mathematics, the very first Standard for Mathematical Practice is that students should “understand problems and persevere in solving them.”1 Whether you are beholden to the Common Core or not, this is certainly something you would wish for your students. Indeed, the National Council of Teachers of Mathematics (NCTM) has been advocating for a central role for problem solving at least since the release of Agenda for Action in 1980, which said, “Problem solving [must] be the focus of school mathematics… .”2
The common instructional model of “I do, we do, you do,” increases student dependence on the teacher and decreases students’ inclination to persevere. How, then, can teachers develop perseverance in problem solving in their students?
First we should clarify what we mean by “problem solving.” According to NCTM, “Problem solving means engaging in a task for which the solution is not known in advance.”3 A task does not have to be a word problem to qualify as a problem — it could be an equation or calculation that students have not previously learned to solve. Also, the same task can be a problem or not, depending on when it is given. Early in the year, before students learn a particular skill, the task could be a problem; later, it becomes an exercise, because now they know how to solve it.
In Japan, math educators have been thinking about how to develop problem solving for several decades. They studied George Polya's How to Solve It,4 NCTM's Agenda for Action, and other documents, and together, using a process called lesson study, they began exploring what it would mean to make problem solving “the focus of school mathematics.” And they succeeded. Today, most elementary mathematics lessons in Japan are organized around the solving of one or a very few problems, using an approach known as “teaching through problem solving.”
“Teaching through problem solving” needs to be clearly distinguished from “teaching problem solving.” The latter, which is not uncommon in the United States, focuses on teaching certain strategies — guess-and-check, working backwards, drawing a diagram, and others. In a lesson about problem solving, students might work on a problem and then share with the class how using one of these strategies helped them solve the problem. Other students applaud, the students sit down, and the lesson ends. These lessons are usually outside the main flow of the curriculum; indeed, they are purposely independent of any curriculum.
In “teaching through problem solving,” on the other hand, the goal is for students to learn precisely that mathematical idea that the curriculum calls for them to learn next.
A “teaching through problem solving” lesson would begin with the teacher setting up the context and introducing the problem. Students then work on the problem for about 10 minutes while the teacher monitors their progress and notes which students are using which approaches. Then the teacher begins a whole-class discussion. Similar to a “teaching problem solving” lesson, the teacher may call on students to share their ideas, but, instead of ending the lesson there, the teacher will ask students to think about and compare the different ideas — which ideas are incorrect and why, which ideas are correct, which ones are similar to each other, which ones are more efficient or more elegant. Through this discussion, the lesson enables students to learn new mathematical ideas or procedures. This approach is represented in Figure 1.
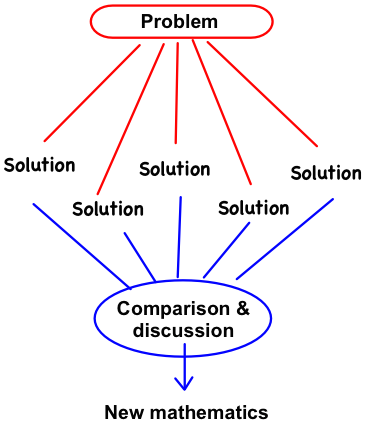
Figure 1
Let's illustrate this with an example from a hypothetical fifth-grade lesson based on the most popular elementary mathematics textbook in Japan. (This textbook has been translated into English as Mathematics International and is available at http://GlobalEdResources.com. 5) During most Japanese lessons, the textbook is closed, but the textbook shows how the authors think the lesson might play out.
When the lesson begins, the blackboard is completely empty. The teacher starts by displaying, either with a poster or using a projector, the picture from the textbook of four different rabbit cages, shown in Figure 2 (it is not uncommon for Japanese elementary students to care for rabbits in several rabbit hutches, so this is a familiar context).

Figure 2 (Mathematics International, Grade 5, p. A93)
“What do you notice about the cages?” the teacher asks. Some students notice that some of the cages are different sizes. The teacher then asks, “Should each cage have the same number of rabbits?” No, say the students, smaller cages should have fewer rabbits, so the rabbits aren't too crowded.
The teacher then displays the pictures in Figure 3. “What do you think?” the teacher asks, as he puts them up one at a time for dramatic effect. “Are these equally crowded, or do you think some cages are more crowded than others?” There is some discussion about the rabbits in cage B, and students decide that just because they are bunched together right now, they probably won't stay that way. Students recognize that cages A and B are the same size, and since cage A has more rabbits (9 vs. 8), it is more crowded. The teacher writes that observation on the board: “When two cages are the same size, the one with more rabbits is more crowded.”
Figure 3 (Mathematics International, Grade 5, p. A93)
“What about the others?” he asks. “How can we decide which are more crowded?” This last question becomes the key mathematical question of the lesson, and the teacher writes it on the board: “Let's think about how to compare crowdedness.” Students copy this problem in their notebooks while he writes.
The teacher gives students a piece of paper with the pictures from Figure 3 to glue in their notebooks and gives them 5 minutes to think about the problem. Several students take a ruler and begin measuring. “Why are you doing that?” the teacher quietly asks one of them. “I want to figure out the area,” the student says. “Oh! You think the area might be important. Write that idea in your notebook.” Other students count the rabbits and decide that B and C are equally crowded because they look like they are the same size, but they are unsure about D.
The teacher stops the students and asks for ideas. He first calls on a student who thinks that B and C are the same size. He records her idea on the board: “Arthi says B and C look like they are the same size and have the same number of rabbits, so they are equally crowded.” A student who found the areas says that they are not. The teacher records this idea on the board: “Karen thinks you need to know the area.” He turns to the first student. “Arthi, what do you think?” he asks. She and other students agree. The teacher posts a table with the areas of the four cages (Figure 4). “Let's copy this table into our notebooks, and think about the problem some more.”
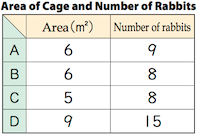
Figure 4 (Mathematics International, Grade 5, p. A94)
Students work independently for another 5 minutes while the teacher monitors their progress, encourages them to keep thinking, and reminds them to record their ideas in their notebook. He anticipates the following five ideas and notes which students are using them:
Idea 1: B and C have the same number of rabbits, but C has a smaller area, so C is more crowded. Unsure about A vs. C.
Idea 2: If you make 5 copies of A and 6 copies of C, they would have the same area (30 m2). A would then have 45 rabbits while C would have 48 rabbits, so C is more crowded.
Idea 3: If you make 8 copies of A and 9 copies of C, they would have the same number of rabbits (72). A would have an area of 48 m2 while C would have an area of 45 m2, so B is more crowded.
Idea 4: Divide: (area) ÷ (# of rabbits) = amount of area per rabbit
Idea 5: Divide: (# of rabbits) ÷ (area) = number of rabbits per unit area
The teacher invites students to explain their ideas to the class, selecting students based on the order above, while he records each idea on the blackboard. He asks students to compare Idea 1 to the thinking used to compare A and B. He writes on the board: “If either the area or the number of rabbits is the same, it's easy to compare.” The student with Idea 2 says, “I found a way to make the area the same,” and explains. This prompts the student with Idea 3 to say, “I used kind of the same approach to make the number of rabbits the same.”
When a student with Idea 4 comes up, she begins, “I decided to divide the area by the number of rabbits.” The teacher stops her. He writes: “(area) ÷ (# of rabbits).” Then he asks the class, “Why is she doing this? Who can explain her thinking?” Another student says, “That gives the amount of area for each rabbit.” He lets the student finish her idea:
A: 9÷6 = 1.5
C: 8÷5 = 1.6
The teacher asks the class to clarify what the 1.5 and 1.6 mean (m2 per rabbit) and what that says about the crowdedness of each cage.
He then invites a student to explain Idea 5: “I divided the other way…”
A: 6÷9 = 0.66…
C: 5÷8 = 0.625
“Why is he doing this?” the teacher asks the class. “What does this 0.66… mean? What does 0.625 mean?” (“Rabbits per square meter,” the students answer.)
The teacher then asks the class to look for similarities across the five ideas, which are all visible on the blackboard. Some students note that Ideas 2 and 3 use multiplication while Ideas 4 and 5 use division, a superficial similarity. But some students notice the more significant connection that 2 and 5 are both about making the area the same, while 3 and 4 are both about making the number of rabbits the same.
“We haven't talked about cage D yet,” the teacher points out. “How shall we compare A, C, and D? Please try using one of these ideas.”
Students work in their notebooks for a few minutes. Students who try using multiplication (Idea 2 or 3) discover that the method is cumbersome. The teacher invites students who used Ideas 4 and 5 to share their calculations, adding them to the lists from before:
Idea 4:
A: 9÷6 = 1.5
C: 8÷5 = 1.6
D: 15÷9 = 1.66… (m2/rabbit) Idea 5:
A: 6÷9 = 0.66…
C: 5÷8 = 0.625
D: 9÷15 = 0.6 (rabbits/m2)
“What do you think about these ideas?” asks the teacher, and students respond, “They are easy!” So the teacher writes a summary on the board, “Using division, it is easy to compare crowdedness.” He asks the students to write a reflection in their notebooks. One student who used multiplication writes, “I tried using multiplication, but dividing is easier. Next time I want to try that.” And the lesson ends.
In the students’ previous experience with comparing quantities, a single quantity was important, such as the number of apples or kilograms or square meters. Their prior experience with division was about finding a missing multiplier or multiplicand, which was itself a single quantity. This problem presented students for the first time with a situation in which two numbers needed to be considered. So by working on a problem about rabbits and cages, students learn that division can be used to compute a new type of quantity, a per unit quantity, that expresses the relationship between rabbits and area and can be used to compare crowdedness. In subsequent lessons, students will see how division can be used to compute other types of per unit quantities, such as the productivity of two farms in crops grown per acre of land or the cost per pencil.
What was the teacher's role in helping students learn this new mathematical idea? He never explained anything to the students, but the task had to be carefully constructed, and the teacher had to be very deliberate in how he directed the lesson, or the lesson wouldn't have worked.
The task was accessible to all students in the beginning by the fact that two cages had the same area (A and B) and two cages had the same number of rabbits (B and C), but since it wasn't clear whether B and C were the same size, students were pushed to think formally about area. And, while using multiplication was feasible for comparing cages A and C, the area of cage D was such that multiplication was cumbersome for comparing all three cages. Students who might have been happy with using multiplication and uncomfortable with the decimal values that result from division were pushed by cage D to appreciate the efficiency of using division.
The teacher's role in the lesson can be compared to the role of a film director, who carefully stages each scene and makes cuts between cameras to create the desired effect. Early in the lesson, the teacher highlighted the idea, raised by students, that equal areas or equal numbers of rabbits made comparisons easier. This was the foundation for the idea of dividing to find a “per unit quantity,” square meters per one rabbit or rabbits per one square meter. By starting with a discussion of incorrect or partially correct ideas and writing them on the board, the teacher valued those ideas. This encourages students to try: Even if they can’t solve the whole problem, they might come up with something to contribute. When a student first suggested the idea of dividing, the teacher asked other students to explain the thinking behind it. This enabled students who did not themselves think of dividing to make the idea their own. And by carefully organizing student ideas on the board (Figure 5), the teacher made it easier for students to compare those ideas with each other and to follow the flow of learning in the lesson.
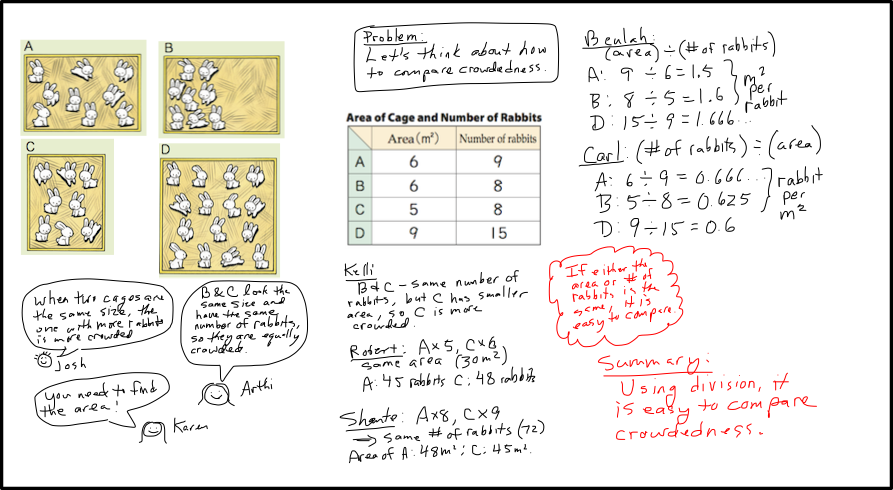
Figure 5 (includes items from Mathematics International, Grade 5, pp. A93-94)
Although the lesson vignette above is fictional, videos of lessons like it can be found at http://tinyurl.com/kuwb4bg. The grade 3 lesson “Multiplication Algorithm” and the grade 5 lesson “Do I Have a Window Seat or an Aisle Seat?” are particularly good, both for the quality of the lessons and for the quality of the videos themselves.
Japanese educators believe that regular lessons that teach through problem solving, interspersed with occasional practice days, help their students learn mathematics more thoroughly than didactic instruction coupled with a greater amount of practice. Certainly Japanese students have performed very well on the TIMSS and PISA international studies of mathematics achievement. But perhaps more important, teaching through problem solving habituates students to being confronted with unfamiliar problems, to struggling at length with those problems, and to learning from those problems. This is a way to cultivate perseverance in problem solving.
Reading this article and watching videos, however, will not equip most teachers to incorporate teaching through problem solving into their practice. The teacher who wishes to do so is faced with several challenges. The first challenge is that few curricula are designed to support such lessons; most are designed to support fairly direct instruction by the teacher. The second problem is that students are not used to learning this way and may resist. And the third problem is that teaching this way is hard. It requires ways of thinking about a lesson that are unfamiliar to almost all U.S. teachers. One needs to be absolutely clear about what the mathematical goal of the lesson is; that goal is never for students to simply solve a problem. One needs to anticipate the various solutions, correct and incorrect, that are likely to come from students, as well as the ways students will get stuck. One needs to plan how the discussion around the various student ideas will address misconceptions and build toward the mathematical goal of the lesson. One needs to think about how the ideas will be organized on the board so that students can easily compare them.
Japanese teachers certainly did not learn to teach this way by reading articles or watching videos. They learned it — and continue to learn it — by trying it, together, one lesson at a time through a process called lesson study.6,7 A full treatment of lesson study would be another article in itself, but U.S. teachers who are interested in learning to teach through problem solving can find more information about lesson study at http://LessonStudyGroup.net and at http://LSAlliance.org. Lesson Study Alliance organizes the annual Chicago Lesson Study Conference, which features live lessons by teachers who are working to incorporate teaching through problem solving into their practice.
Notes
1. National Governors Association Center for Best Practices, Council of Chief State School Officers, Common Core State Standards for Mathematics (Washington, DC: National Governors Association Center for Best Practices, Council of Chief State School Officers, 2010); online at www.corestandards.org/math/.
2. National Council of Teachers of Mathematics, An Agenda for Action: Recommendations for School Mathematics of the 1980s (Washington, DC: NCTM, 1980); online at www.nctm.org/standards/content.aspx?id=17278.
3. National Council of Teachers of Mathematics, Principles and Standards for School Mathematics (Washington, DC: NCTM, 2000); online at http://www.nctm.org/standards/content.aspx?id=16909.
4. George Polya, How to Solve It: A New Aspect of Mathematical Method (Princeton, NJ: Princeton University Press, 1945).
5. T. Fujii and S. Iitaka, Mathematics International, Grades 1-6 (Tokyo: Tokyo Shoseki Co., Ltd., 2012).
6. Akihiko Takahashi, “Implementing Lesson Study in North American Schools and School Districts” (no date); online at http://hrd.apec.org/images/a/ae/51.2.pdf.
7. Akihiko Takahashi and Makoto Yoshida, “Ideas for Establishing Lesson-Study Communities.” Teaching Children Mathematics, May 2004.